téléchargez ce document au format pdf

Ce que vous devez savoir pour faire ce calcul :

1. - Règle concernant la distance lampe/châssis :
La distance pour que l'insolation soit uniforme et optimisée doit être égale à la diagonale de l'écran.

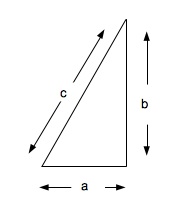
2. - Formules pour calculer la diagonale :
a2 + b2 = c2

3. - Formule pour calculer le nouveau temps de pose :
Divisez la nouvelle distance par l'ancienne distance,
puis multipliez le résultat par l'ancien temps de pause.



Application :

Temps de pause actuel : Temps de pose : 3 minutes (soit 180 secondes)
Distance châssis/lampe : 1,40 mètre (soit 140 cm).

1. - faire le calcul pour un écran 40 x 80 cm.

1°) Calcul de la nouvelle distance entre le châssis et la lampe d'insolation, je dois donc calculer la diagonale de l'écran 40 x 80 cm.
J'applique la formule :
402  = 1600
802  = 6400
1600 + 6400 = 8000 (8000 représente le carré de la diagonale ou le carré de « c » dans la formule, donc je dois rechercher la racine carrée de 8000)
Ѵ8000 (racine carrée de 8000) = 89,4427191
Nouvelle distance = 89,4427191 cm
2°) Calcul du nouveau temps de pose.
J'applique la formule :
nouvelle distance (89,4427191 cm) divisée par l'ancienne distance (140 cm – voir l'énoncé)
89,4427191 :  140 = 0,638876565
Le résultat (0,638876565) est multiplié par l'ancien temps de pose (180 secondes – voir l'énoncé)
0,638876565 X 180 = 114,9977817 secondes (soit 115 secondes)



2. - faire le calcul pour un écran 140 x 180 cm.
1°) Calcul de la nouvelle distance entre le châssis et la lampe d'insolation, je dois donc calculer la diagonale de l'écran 140 x 180  cm.
J'applique la formule :
1402  = 19600
1802  = 32400
19600 + 32400 = 52000 (52000 représente le carré de la diagonale ou le carré de « c » dans la formule, donc je dois rechercher la racine carrée de 52000)
Ѵ52000 (racine carrée de 52000) = 228,035085
Nouvelle distance = 228,035085 cm
2°) Calcul du nouveau temps de pose.
J'applique la formule :
nouvelle distance (228,035085 cm) divisée par l'ancienne distance (140 cm – voir l'énoncé)
228,035085 :  140 = 1,62882203571429
Le résultat (1,62882203571429) est multiplié par l'ancien temps de pose (180 secondes – voir l'énoncé)
1,62882203571429 X 180 = 293,187966428572 secondes (soit 293 secondes)

Constat : plus l'écran est grand, plus le temps de pose est grand

Conseils :
Utilisez toujours les mêmes unités pour faire les comparaison (soit des cm, soit des mm, etc.)
Convertissez le temps en seconde pour faire les calculs.